

This tutorial uses an example study of multicomponent square-well particles to introduce several topics:
Although this tutorial looks at a multicomponent square-well fluid, it provides you with all of the knowledge you need to study any multicomponent system.

A rendering of the binary square-well system studied.
For the purpose of the tutorial, we'll want to simulate a mixture of square-well molecules. If you want to learn more about the square-well potential, its parameters, and how it corresponds to realistic intermolecular interactions please see the reference entry linked below.
We're going to study a binary mixture of $N=4000$ square-well molecules. We'll have a larger species, $A$, and a smaller species, $B$ (see right).
We will again use periodic boundary conditions, and these are described in the following reference entry.
The mixture we will study has a hard-core diameter ratio of $\sigma_A/\sigma_B=2$ and a mass ratio proportional to their volumes $m_A/m_B=\sigma_A^3/\sigma_B^3=8$. Both molecules have the same well-width factor $\lambda_A=\lambda_B=1.5$. For interactions between species we'll use the additive rule. For example, between species A and B the interaction diameter is $\sigma_{AB}=\left(\sigma_A+\sigma_B\right)/2$. We'll want to be able to study the mixture over a range of densities, temperatures, and concentrations.

An illustration of the variables of the system.
The dynamod/dynarun commands we will run are
#Create the monocomponent system
dynamod -m 1 -C 10 -d 0.5 --i1 0 -r 1 -o config.start.xml
#Now edit config.start.xml by hand to convert it into a multicomponent system
#...
#Compress the multicomponent system to a higher density
dynarun config.start.xml --engine=3 --target-pack-frac 0.3 -o config.compressed.xml
#Add a thermostat, to allow us to control the temperature
dynamod config.compressed.xml -T 1.5 -Z -o config.thermostatted.xml
#Equilibrate the system using the thermostat to set the temperature
dynarun config.thermostatted.xml -c 1000000 -o config.thermostatted.xml
#Now collect data on the system
dynamod config.thermostatted.xml -T 0 -Z -o config.prerun.xml
dynarun config.prerun.xml -c 1000000 -o config.end.xml -L MSD
Once this is done, we'll disable the thermostat and perform another run to collect output data and include some output plugins.
dynamod config.thermostatted.xml -T 0 -Z -o config.prerun.xml
dynarun config.prerun.xml -c 1000000 -o config.end.xml -L MSD
We'll now look in detail at these commands, in particular how the configuration file was edited by hand into a multicomponent system.
When you first start using DynamO, it is not really practical to try to create a configuration file from scratch. It is much simpler and convenient to take an existing configuration, which is close to the system you wish to study, and to modify it. Once you are familiar with DynamO and the XML file format you may write your own tools to generate configuration files in the programming language of your choice (see the reference on XML libraries for more information on this).
Following the last tutorial, we can see that square-well fluids can be made using dynamod's packing mode 1. We can get some more information on this mode using the following command:
dynamod -m 1 --helpAnd a detailed description of the modes options will be outputted on screen:
...
Mode 1: Mono/Multi-component square wells
Options
-C [ --NCells ] arg (=7) Set the default number of lattice unit-cells in each direction.
-x [ --xcell ] arg Number of unit-cells in the x dimension.
-y [ --ycell ] arg Number of unit-cells in the y dimension.
-z [ --zcell ] arg Number of unit-cells in the z dimension.
--rectangular-box Set the simulation box to be rectangular so that the x,y,z cells also specify the simulation aspect ratio.
-d [ --density ] arg (=0.5) System density.
--i1 arg (=FCC) Lattice type (0=FCC, 1=BCC, 2=SC)
--f1 arg (=1.5) Well width factor (also known as lambda)
--f2 arg (=1) Well Depth (negative values create square shoulders)
--s1 arg (monocomponent) Instead of f1 and f2, you can specify a multicomponent system using this option. You need to pass the the parameters for each species as follows --s1 "diameter(d),lambda(l),mass(m),welldepth(e),molefrac(x):d,l,m,e,x[:...]"
...You might notice that this mode can create a multicomponent system for us using the first string option (--s1), but we'll create it by hand here to understand the process.
Lets start by making a monocomponent mixture of square-wells using the following command:
dynamod -m 1 -C 10 -d 0.5 --i1 0 -r 1 -o config.start.xmlThe options passed here are discussed in detail in tutorial 2. The most significant value is the total number of particles is $N=4000$ (-C 10). An example of the configuration file is available below (it is a large XML file, so your browser may take some time to display it).
This system has the 4000 particles we're looking for, but we'll need to convert a fraction of these to another species to make the multicomponent square-well system we wish to study. In the following sections we look at what needs to be done to perform this conversion, and learn how DynamO handles multiple interactions.
If you open the config.start.xml file in a text editor, you'll notice that there is only one Species defined:
<DynamOconfig>
<Simulation>
<Genus>
<Species Mass="1" Name="Bulk" Type="Point">
<IDRange Type="All"/>
</Species>
</Genus>
</Simulation>
</DynamOconfig>
If we want to study a binary system, we'll need to define two Species to be able to get per-species results in the output data. Using two Species also provides a convenient way to specify the different masses of the two types of particles. Lets assume we want to convert the first 100 particles in the configuration file to Species "A" and have the rest as Species "B", we can change the file to:
<DynamOconfig>
<Simulation>
<Genus>
<Species Mass="1" Name="A" Type="Point">
<IDRange Type="Ranged" Start="0" End="99"/>
</Species>
<Species Mass="0.125" Name="B" Type="Point">
<IDRange Type="Ranged" Start="100" End="3999"/>
</Species>
</Genus>
</Simulation>
</DynamOconfig>
You should notice that we've reduced the mass of the smaller particles (type B) to match the ratio $m_A/m_B=8$. This implies that we'll also need to effectively shrink the diameter of the particles which are becoming Species B. Instead, we could have increased the mass of the larger particles (type A) to satisfy this ratio; but this would have meant that we would also have to increase their diameter. The problem with increasing diameters of particles by hand is that you may accidentally cause nearby particles to overlap. We must be careful to avoid creating overlapping cores, as the dynamics are undefined in these cases. DynamO is stable to overlaps and may eventually resolve these errors but it is not guaranteed in all cases. We have also deliberately kept a mass at a value of 1, as this corresponds to a set of reduced units (see the FAQ on the units of DynamO)
You should also notice that the IDRange of Type "Ranged" is an inclusive range of particle ID's. The particle ID's start with zero and end on 99; therefore, the first Species tag corresponds to the first 100 particles in the configuration file. For more information on the "Ranged" IDRange tag, please see the reference:
In the next section we'll take a look at setting up all of the Interactions of the system.
In the original file, only one square-well Type Interaction is defined:
<DynamOconfig>
<Simulation>
<Interactions>
<Interaction Type="SquareWell" Diameter="1" Elasticity="1" Lambda="1.5" WellDepth="1" Name="Bulk">
<IDPairRange Type="All"/>
<CaptureMap>
<Pair ID1="0" ID2="336" val="1"/>
<Pair ID1="0" ID2="756" val="1"/>
...
</CaptureMap>
</Interaction>
</Interactions>
</Simulation>
</DynamOconfig>
Here, we will use three separate Interaction tags to input the parameters of the three types of interactions between all species (A-A, A-B, and B-B). We were very careful to shrink the mass of type "B" particles so that, in order to obtain the ratio $\sigma_A/\sigma_B=2$, the large particles will have a diameter of $\sigma_A=1$ and the small particles a diameter of $\sigma_B=0.5$. An example implementation using these diameters is given below:
<DynamOconfig>
<Simulation>
<Interactions>
<Interaction Type="SquareWell" Diameter="1" Elasticity="1" Lambda="1.5" WellDepth="1" Name="AAInteraction">
<IDPairRange Type="Single">
<IDRange Type="Ranged" Start="0" End="99"/>
</IDPairRange>
</Interaction>
<Interaction Type="SquareWell" Diameter="0.75" Elasticity="1" Lambda="1.5" WellDepth="1" Name="ABInteraction">
<IDPairRange Type="Pair">
<IDRange Type="Ranged" Start="0" End="99"/>
<IDRange Type="Ranged" Start="100" End="3999"/>
</IDPairRange>
</Interaction>
<Interaction Type="SquareWell" Diameter="0.5" Elasticity="1" Lambda="1.5" WellDepth="1" Name="BBInteraction">
<IDPairRange Type="All"/>
</Interaction>
</Interactions>
</Simulation>
</DynamOconfig>
The first Interaction entry handles the interactions between Species "A" particles. A special "Single" type IDPairRange is used to convert a single IDRange, which identifies all of the type A particles, into a IDPairRange describing all pairings of type A particles.
The second Interaction entry corresponds to the inter-Species Interactions between type A and type B particles. Here, another type of IDPairRange is used which takes two IDRanges and creates a IDPairRange which matches all pairings between them. The diameter of the Interaction is worked out using the additive rule: \[\sigma_{AB}=\left(\sigma_A+\sigma_B\right)/2=\left(1+0.5\right)/2=0.75\] Technically, the well-width factor $\lambda$ is also calculated using the additive rule, but as both Species have the same value we have $\lambda_{AB}=\lambda_A=\lambda_B=1.5$.
The final Interaction represents the intra-Species interactions between the type B particles. Surprisingly, this has an "All" type IDPairRange tag which maps to all possible pairings of particles in the system. This works due to the way that DynamO searches for Interactions. DynamO moves down the list of Interactions in order testing against each Interaction for a match. The first match is the one that is returned! So, this last tag actually matches all pairs except for those that match above. The only pairs which are left are the B-B pairings.
In the third Interaction, we could have also used the following IDPairRange instead of the "All" type:
<IDPairRange Type="Single">
<IDRange Type="Ranged" Start="100" End="3999"/>
</IDPairRange>
A good reason for using the catch-"All" Interaction in the end is that in complex systems with unusual Interaction IDPairRanges it can be quite hard to define which particles are actually left over. Using an "All" rule at the end and catching the complex interactions makes it simpler to implement.
Although the example Interactions listed above are suitable for our system, it is obvious there is more than one way to specify the Interactions. For example, we could specify the B-B Interaction first instead. A general rule for DynamO is that the simplest configuration files are the fastest but the way in which the Interactions are specified will usually not make much difference to the performance of DynamO, so use whatever is most convenient for you.
You should notice that the CaptureMap tag in the original mono-component configuration file has been deleted and that the new Interaction tags do not contain them. This is deliberate as we want DynamO to rebuild the CaptureMap as we have changed the Interaction parameters. For more information on CaptureMaps and why deleting it is required, please see the reference linked below.
The configuration has now been modified to a two-component square-well system and an example of the finished configuration is available below.
We'll now look at converting this into a high density configuration and how to thermostat the temperature.
A 10:1 size-ratio low-density binary square-well system under
compression.
View configuration file
To create the binary system we had to shrink one set of particles to avoid causing any overlaps or invalid states. Unfortunately, this results in a low-density configuration (for example see right). The low-density behaviour of fluids is fairly well-understood as it approaches that of an ideal gas. Most of the interesting behaviour we wish to explore through simulation appears at higher densities, so we need a method to generate high-density systems.
To access high density systems while avoiding generating invalid states, DynamO implements the linear compression algorithm first proposed by Woodcock[paper], but later popularised by Lubachevsky and Stillinger[paper]. This is a mode of simulation where all particles grow in size over time. At the end of the growth run, the dimensions are all rescaled so that the particles have the same initial size, but the simulation box has shrunk proportionally.
To carry out the compression, use the engine option of dynarun to use the compression engine. You also set the end point of the compression using either the --target-pack-frac or the --target-density option. If you don't use these options, the compression will keep running and you'll have to manually stop the simulation by pressing ctrl-c.
dynarun config.start.xml --engine=3 --target-pack-frac 0.3 -o config.compressed.xmlOnce this command completes, we should have a compressed configuration at a packing fracton of $0.3$. Please see this FAQ on why we decided to set the packing fraction, not the number density of the system.
A video of an example compression run is given to the right (its a $\sigma_A/\sigma_B=10$ system to exaggerate the effect). The simulation ends automatically once the target number density or packing fraction is reached which may take some time. If the system appears to get "stuck" (the simulation time is not increasing), then it might be wise to stop the compression run, rescale the particle velocities, and to run a normal simulation for a while to allow the system to become unstuck/relax.
During compression you should be able to observe that the temperature and internal energy is varying significantly. This is due to the changes in internal energy and the work performed by the compression process. The compression process also slows down over time and any heating causes more events per unit time slowing it even further.
You may consider stopping the compression periodically and rescaling the temperature as it can accelerate the compression. You can find out how to stop any simulation while it is running in this FAQ. To rescale the temperature of a configuration file we can use the following dynamod command:
dynamod config.compressed.xml -r 1 -o config.compressed.xmlThis will rescale the velocities of the particles in the system so that the current temperature is 1 (set by the -r option). Please note, as discussed in the previous tutorial this option does not thermostat the temperature. In systems such as the square-well fluid studied here we will need to use a thermostat to control the temperature.
We'll add a thermostat to control the temperature to $k_B\,T=1.5$ and then equilibrate the system.
dynamod config.compressed.xml -T 1.5 -Z -o config.thermostatted.xml
dynarun config.thermostatted.xml -c 1000000 -o config.thermostatted.xml
Once this is done, we'll disable the thermostat and perform another run to collect output data and include some output plugins.
dynamod config.thermostatted.xml -T 0 -Z -o config.prerun.xml
dynarun config.prerun.xml -c 1000000 -o config.end.xml -L MSD -L RadialDistribution
Again, this might not have an absolutely correct temperature due to the thermostat being disabled, but we need to disable it to measure dynamical properties.
Some output plugins are classed as ticker type plugins (see the reference). This includes the RadialDistribution plugin which we enabled with a -L RadialDistribution option to dynarun. These plugins only collect data at discrete points or "ticks" in time, rather than over the duration of the simulation.
These types of output plugins can sometimes significantly slow down the simulation, so it is advised not to sample too frequently. Here, we've chosen to sample every 0.1 units of simulation time (set by the -t 0.1 option). If we didn't set this option, the system would sample once every mean free time (determined from the last run of the configuration). For this simulation this will result in around 30 ticks which, combined with the fact that radial distribution functions are averaged over every particle, should give enough samples for a fairly accurate determination of the data.
We'll now take a look at the results.
The first point to process is to establish if the temperature is around the required value:
<Temperature Mean="1.4874191074455181" MeanSqr="2.2124672458327441" Current="1.4955841973958153" Min="1.4614175307291486" Max="1.5130841973958153"/>
Again, as discussed in tutorial 4, there is some drift but this is not unexpected.
We can see that the addition of a second Species to the system has resulted in some additional information to be collected. For example, the MSD plugin has collected per-species diffusion coefficients:
<MSD>
<Species Name="A" val="1.6847332769239043" diffusionCoeff="0.094944658505663653"/>
<Species Name="B" val="3.845481903543519" diffusionCoeff="0.21671559001213933"/>
</MSD>
If we also run dynatransport on the system, we can see that there are additional diffusive transport coefficients collected and they are no-longer zero.
dynatransport output.xml -s 0.05 -c 0.3 -v
ShearViscosityL_{\eta,\eta}= 1.46849095852 +- 0.0 <R>^2= 0.997803923764
BulkViscosityL_{\kappa,\kappa}= 5.96424257036 +- 0.0 <R>^2= 0.98471945448
ThermalConductivityL_{\lambda,\lambda}= 43.0867400675 +- 0.0 <R>^2= 0.999308834014
ThermalDiffusionL_{\lambda,A}= -0.0538445647777 +- 0.0 <R>^2= 0.974926102908
ThermalDiffusionL_{\lambda,B}= 0.0538445647777 +- 0.0 <R>^2= 0.974926102908
MutualDiffusionL_{B,B}= 0.00259576820261 +- 0.0 <R>^2= 0.999630761695
MutualDiffusionL_{A,B}= -0.00259576820261 +- 0.0 <R>^2= 0.999630761695
MutualDiffusionL_{A,A}= 0.00259576820261 +- 0.0 <R>^2= 0.999630761695
Please be careful about using these results as the above correlation window, $\Delta t\in\left[0.05,0.3\right]$, was not rigourously determined. Also, as there are now many molecular processes occuring each with different timescales, it is more complex to determine when short-time effects cease to dominate the correlation functions.
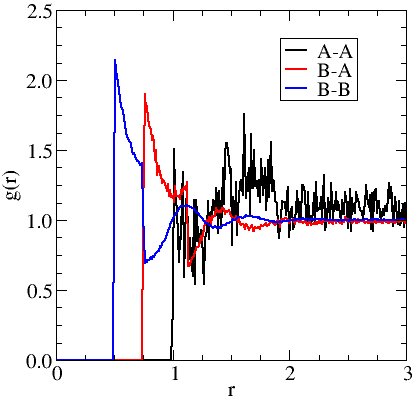
A plot of the three radial distribution functions for the binary square-well system studied.
In this tutorial, we introduced a new ticker-type plugin for collecting the radial distribution function. The data for this plugin is stored in the RadialDistribution tag in the output file:
<RadialDistribution SampleCount="30">
<Species Name1="A" Name2="A" Origins="3000" Samples="297000">
0.01 0
0.02 0
0.029999999999999999 0
...
</Species>
<Species Name1="A" Name2="B" Origins="3000" Samples="11700000">
0.01 0
0.02 0
0.029999999999999999 0
...
</Species>
<Species Name1="B" Name2="A" Origins="117000" Samples="11700000">
0.01 0
0.02 0
0.029999999999999999 0
...
</Species>
<Species Name1="B" Name2="B" Origins="117000" Samples="456183000">
0.01 0
0.02 0
0.029999999999999999 0
...
</Species>
</RadialDistribution>
If we cut out each of the columns of data and plot them together we have the graph presented to the right. We can see that the sampling of the A-A distribution has poor statistics when compared to the B-B, due to the relatively small number of A type particles in the system when compared to the B-type. This is confirmed when we compare the values of the Samples attribute for each graph. We can attempt to mitigate this by increasing the "tick" rate to collect more samples or by extending the simulation time. Increasing the tick rate is cheaper but longer simulations should give better sampling overall.
We can also see the discontinuities in $g(r)$ caused by the discontinuity in the intermolecular potential at $r=\sigma$ and $r=\lambda\,\sigma$ for each curve.
We've now introduced multiple Species and Interactions, allowing a wide range of mixtures to be studied and opening the door to the construction of more complex systems. Ticker output plugins are introduced as a new mechanism used to collect data on the simulation, particularly for "expensive" computations like the RadialDistribution plugin. Later tutorials will now focus on increasing the complexity of the simulations.
Page last modified: Thursday 29th July 2021